
Dostaję nieznaną monetę, wykonuję nią trzy rzuty i za każdym razem wypada orzeł. Jakie jest prawdopodobieństwo, że w następnej próbie również wypadnie orzeł? Czy ta moneta w ogóle jest wyważona? Jak to wyliczyć i sprawdzić?
Rzut monetą
W tym poście przedyskutujemy sprawę z dwóch punktów widzenia - nieufnego Kleofasa i doświadczonej Leokadii. Z jednej strony, argumentuje Kleofas, dostaliśmy nieznaną monetę i przeprowadziliśmy trzy eksperymenty. Szansa na wyrzucenie orła w trzech rzutach to tylko \(0.5^3 \approx 13 \%\) więc jest duże prawdopodobieństwo, że moneta nie jest dobrze wyważona. W takim razie, w następnym rzucie jest większa szansa, że znowu wypadnie orzeł…
Z tą analizą może nie zgodzić się Leokadia… Rachunek i intuicja Kleofasa wydają się poprawne jednak coś wydaje się nie tak - monety ZWYKLE SĄ wyważone więc dokonanie jedynie trzech pomiarów to stanowczo za mało aby podważyć to przekonanie… Bez dodatkowych testów, ciężko rozsądzić pomiędzy tymi dwoma punktami widzenia… I nie wydaje się, żeby ktokolwiek miał tutaj rację. W tym artykule pokażę jak pogodzić te podejścia jako… dwie strony tej samej monety.
Pierwszy element: model rzutu monetą
Potrzebujemy probabilistycznego modelu rzutu monetą. Pod tą poważną nazwą skrywa się po prostu funkcja prawdopodobieństwa, która opisze serię rzutów jedną monetą za pomocą jakiegoś parametru dobroci monety \(q\). Jeden rzut możemy opisać poprzez próbę Bernoulliego:
\[p_i = \left \{ \begin{array}{c} q, \quad \text{i = orzeł} \\ (1-q) \quad \text{i = reszka} \end{array} \right .\]
gdzie \(q\) to prawdopodobieństwo wyrzucenia orła zaś z prawdopodobieństwem \(1-q\) wypadnie reszka. Gdy \(q=1/2\), moneta jest wyważona… ale w naszym modelu oczywiście nie zakładamy jej wartości - to parametr modelu, który musimy jakoś znaleźć! Zakładając niezależność pomiędzy rzutami, wielokrotny rzut tą samą monetą zapiszemy jako iloczyn \(n\) takich prawdopodobieństw:
\[P(i_1, ..., i_n) = \prod_{k=1}^n p_{i_k},\]
gdzie każdy \(i_j\) indeks może przybrać wartość orzeł lub reszka. Teraz szukamy prawdopodobieństwa, że w \(k\) z tych \(n\) rzutów wypadnie orzeł. Zapiszemy to jako dosyć skomplikowaną sumę:
\[\pi_n(\text{k orłów} \vert q) = \sum_{i_1...i_n} \sum_\sigma \overbrace{\delta_{i_{\sigma(1)},1} \cdots \delta_{i_{\sigma(k)},1}}^{\text{k orłów}} \overbrace{\delta_{i_{\sigma(k+1)},0} \cdots \delta_{i_{\sigma(n)},0}}^{\text{n-k reszek}} P(i_1...i_n),\]
gdzie \(\sigma\) to wszystkie permutacje \(k\) sposród \(n\) indeksów a człony \(\delta_{i,1}\) wybierają orły/reszki dla \(i\)-tego indeksu. Użyłem tutaj indeksów \(i=1\) dla orła oraz \(i=0\) dla reszki. Używając znanego wyniku na permutacje oraz rozwijając każdy człon w łącznym prawdopodobieństwie \(P\), dostajemy ostateczny wynik:
\[\pi_n(\text{k orłów} \vert q) = \binom{n}{k} q^k (1-q)^{n-k},\]
czyli rozkład dwumianowy.
Drugi element: twierdzenie Bayesa
Aby pogodzić Kleofasa i Leokadię, będziemy potrzebować twierdzenia Bayesa:
\[P(\text{param} \vert \text{data}) P(\text{data}) = P(\text{data} \vert \text{param}) P(\text{param})\]
który jest używany jako narzędzie do aktualizacji naszych założeń w oparciu o nowe dane. W takim podejściu, naszym zadaniem jest obliczenie \(P(\text{param} \vert \text{data})\) tj. rozkładu wynikowego (a posteriori), który opisuje naszą wiedzę po uwzględnieniu danych \(\text{data}\). W tym celu, potrzebujemy
-
rozkładu zaczątkowego (a priori) \(P(\text{param})\), który reprezentuje naszą początkową wiedzę lub pewne przekonanie o problemie,
-
wiarygodnością \(P(\text{data} \vert \text{param})\) która odzwierciedla model naszego zjawiska,
-
wiarygodności brzegowej \(P(\text{data})\), która jest wynikiem wycałkowania rozkładu zaczątkowego i wiarygodności \(P(\text{data}) = \int d(\text{param}) P(\text{data} \vert \text{param}) P(\text{param})\).
Ale co z tą monetą?
Po tej abstrakcyjnej dyskusji, wróćmy do naszej monety. Wiarygodnością będzie w tym przypadku rozkład dwumianowy \(P(\text{data} \vert \text{param}) \to \pi_n(\text{k orłów}\vert q)\) gdzie parametrem będzie prawdopodobieństwo wylosowania orła \(q\). Rozkładem zaczątkowym tego prawdopodobieństwa zaś będzie rozkład beta:
\[P(\text{param}) \to f_{\alpha,\beta}(q) = N_{\alpha,\beta} q^{\alpha - 1} (1-q)^{\beta-1}\]
z czynnikiem normalizacyjnym \(N_{\alpha,\beta} = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\).
Wybór rozkładu zaczątkowego nie jest przypadkowy - z jednej strony, dla parametrów \(\alpha=\beta=1\) redukuje się on do rozkładu jednostajnego, który odpowiada podejściu Kleofasa do problemu monety - całkowitej ignorancji co do jej wyważenia. Z drugiej, jest to rozkład sprzężony do rozkładu dwumianowego co oznacza, że rozkład wynikowy jest także rozkładem beta i może być wyliczony explicite i jest równy:
\[P(q \vert \text{k orłów}, \text{n-k reszek}) = f_{\alpha + k,\beta + n-k}(q),\]
z nowymi parametrami \(\alpha' = \alpha + k\), \(\beta' = \beta + n-k\).
Wróćmy do dwóch bohaterów, Kleofasa i Leokadii. Co tak naprawdę różni te dwa podejścia? Jest to wybór rozkładu zaczątkowego… Kleofas jest nieufny co do natury monet - stąd jego rozkład zaczątkowy może być jednostajny tj. odpowiadać \(\alpha_K = \beta_K = 1\). Leokadia zaś jest dużo pewniejsza co do natury monet - w końcu nie raz używała ich lub widziała jak ktoś inny bawi się monetą jako sposobem rozwiązywania sporów. Zatem jej rozkład zaczątkowy powinien być dużo bardziej skupiony wokół \(q = 1/2\)… Jak to jednak zrobić? Okazuje się, że dla dużych wartości \(\alpha_L = \beta_L \gg 1\), rozkład skupia się coraz bardziej wokół tej “wyważonej” wartości. Wybór tej wartości jest subiektywny i zostawimy go Leokadii.
Zobaczmy teraz jak różnie wyglądają rozkłady dla ostrożnego Kleofasa oraz dla pewnej swoich monet Leokadii:
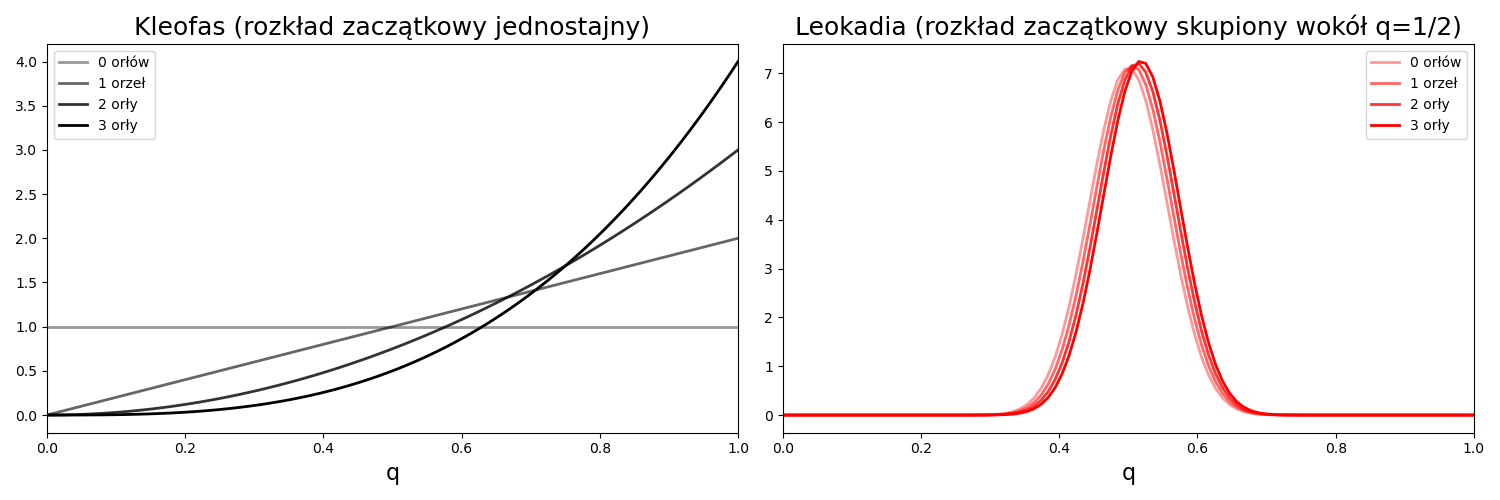
Dla Kleofasa, trzy pomiary wystarczają aby zmienić w dużym stopniu rozkład wartości \(q\). Z drugiej strony, wynik Leokadii nie wydaje się bardzo wzruszony przez trzy pomiary i nadal rozkład aprioryczny jest w dużej mierze skupiony wokół \(q=1/2\). Poniżej widzimy jak różna jest ewolucja rozkładów dla Kleofasa i Leokadii w miarę wzrastającej liczby wyrzuconych orłów:
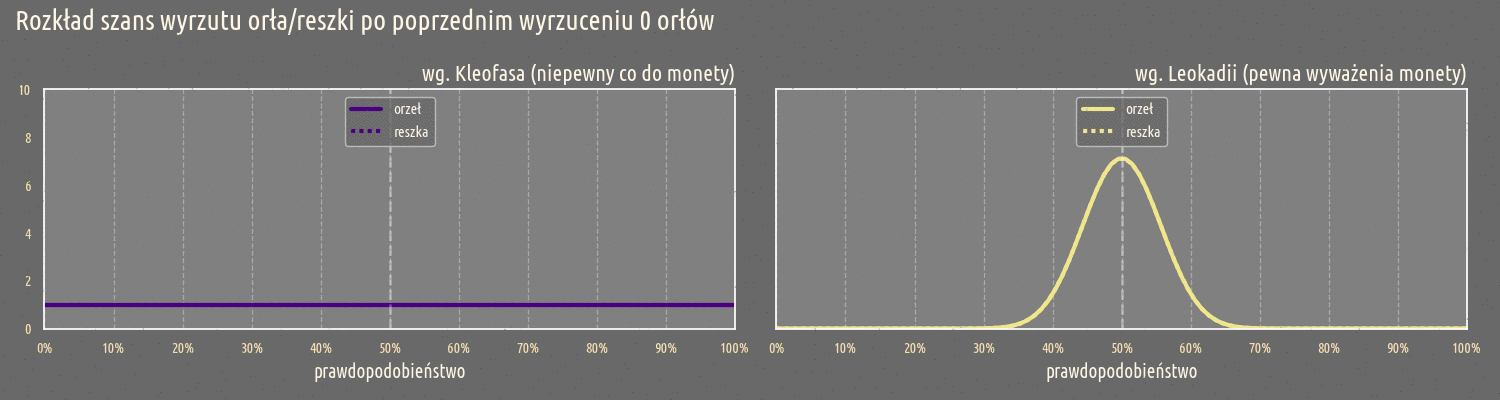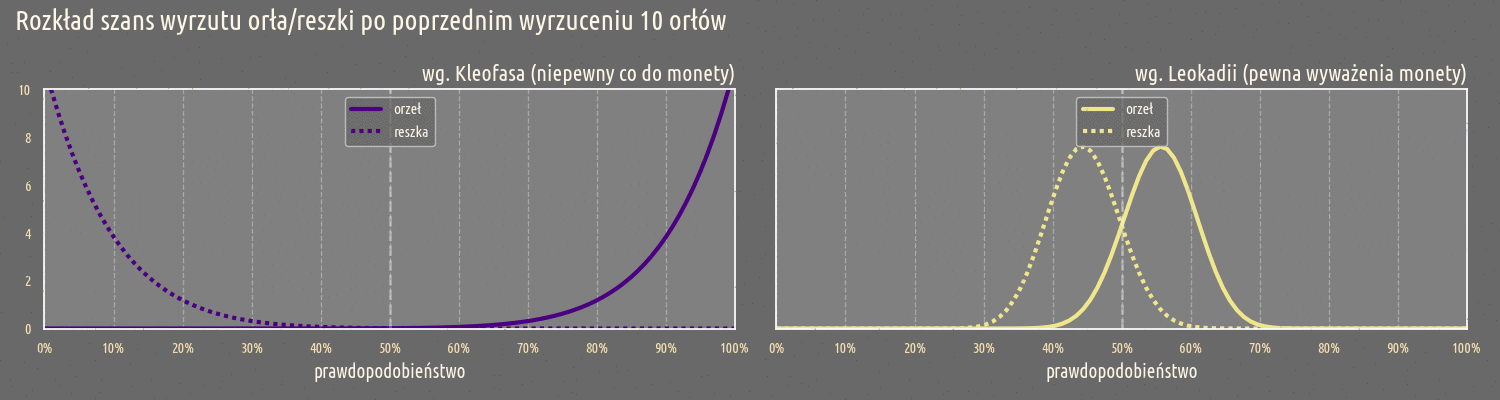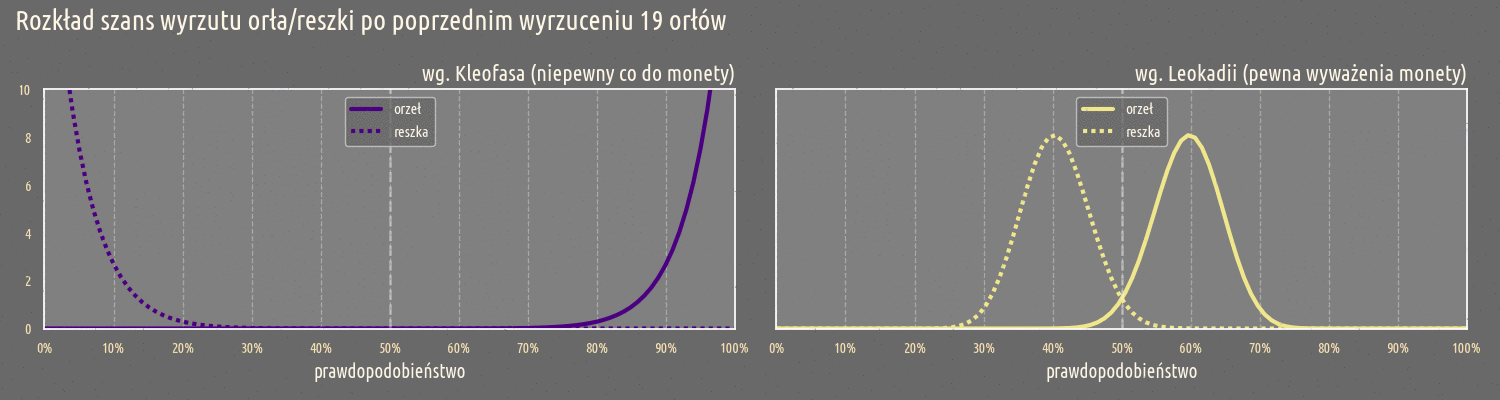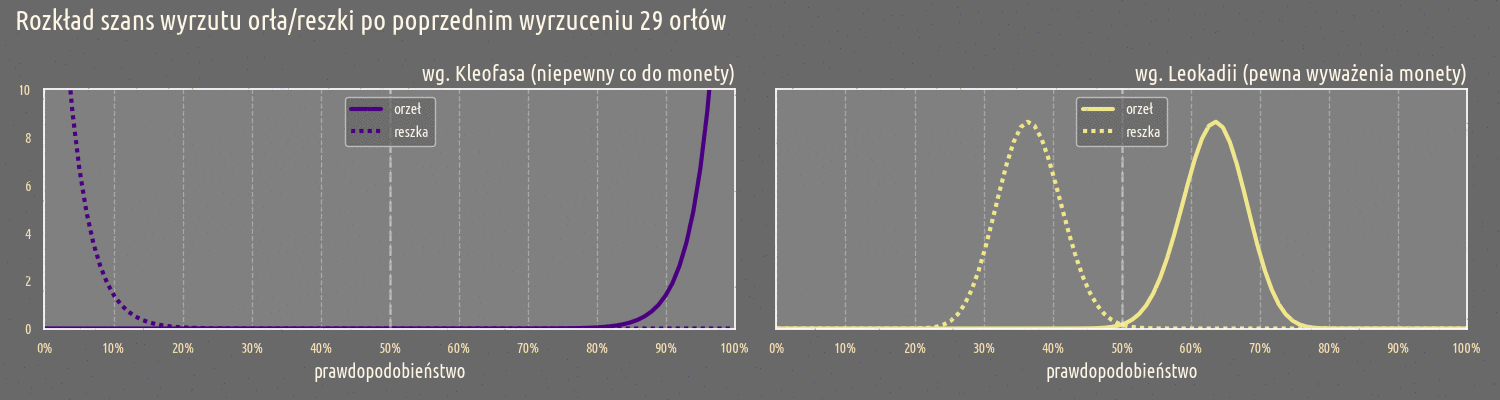
Ta tendencje jest także widoczna przy oczekiwanych prawdopodobieństwach w miarę wzrastającej liczby wyrzuconych orłów:
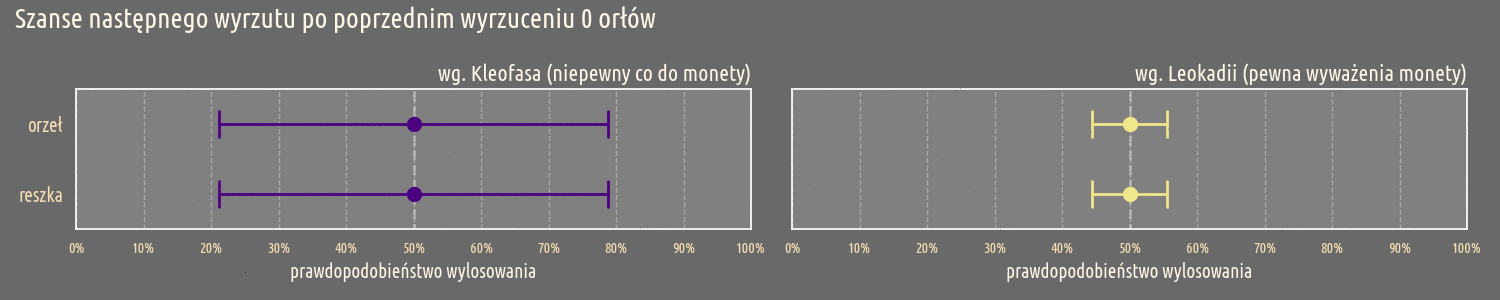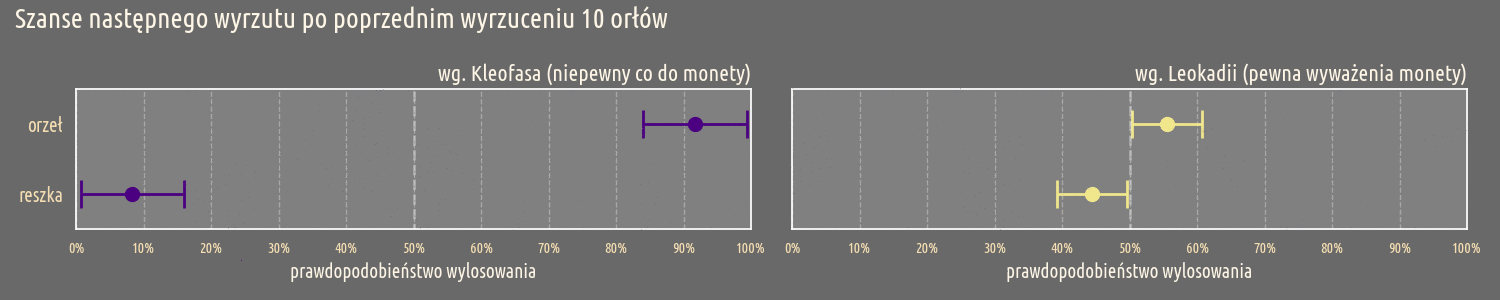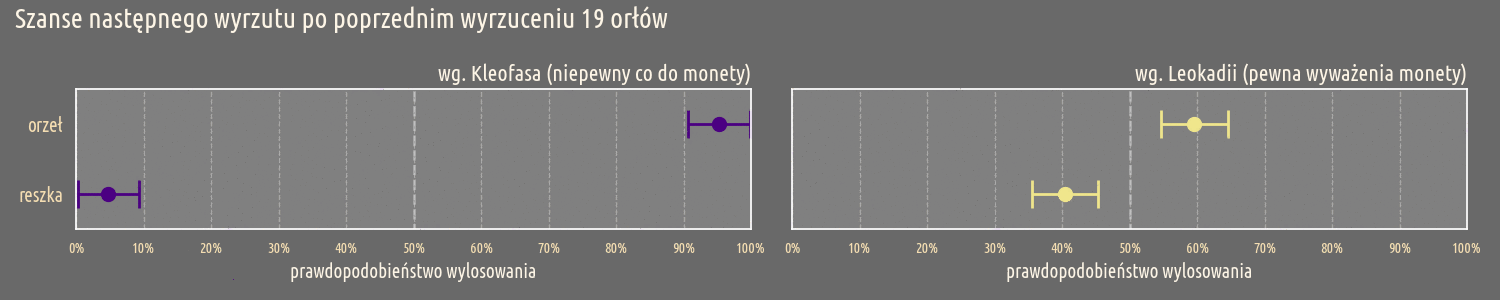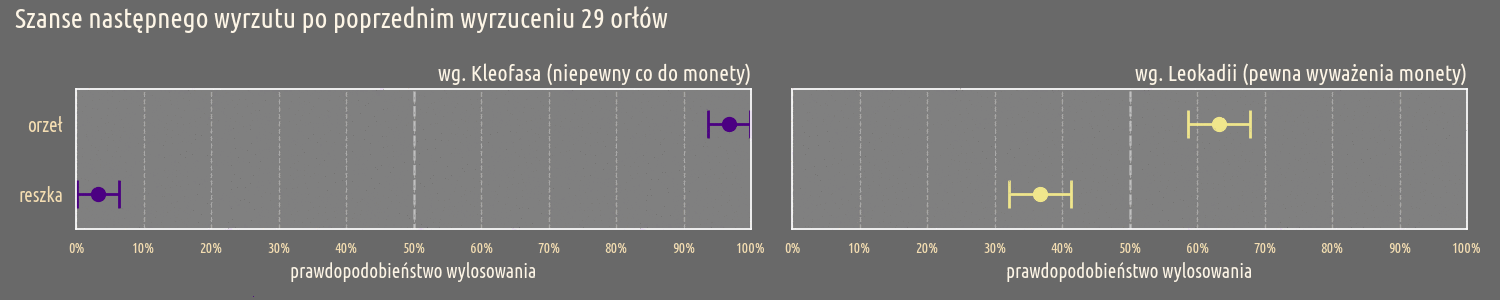
Przed dokonaniem pomiarów, zarówno Kleofas jak Leokadia oczekują, że moneta będzie wyważona. Jednak widać od początku, że niepewność Kleofasa jest zdecydowanie większa od niepewności Leokadii. Ta tendencja utrzymuje się w miarę przeprowadzania kolejnych pomiarów, Kleofas już po dwóch wyrzuconych orłach nie może mieć przekonania o wyważeniu monety. Dla Leokadii ta granica jest dużo dalej i dopiero przy 10 wyrzuconych orłach, jej pewność co do wyważenia monety jest podważona.
Jaki będzie następny rzut?
Dobrze, zatem co się najprowdopodobniej stanie w czwartym rzucie? Dla Kleofasa, orzeł wypadnie z prawdopodobieństwem \(\approx 80\%\), dla Leokadii ta szansa to jedynie \(\approx 52\%\). Nasze wstępne założenia są kluczowe.
Wnioski
- Wnioskowanie Bayesowskie pozwala na ilościowe podejście do badań prawdopodobieństw
- Wnioskowanie zależy w znaczący sposób od początkowych, subiektywnych założeń